Chapter 2 Basic Perceptions about Markets Part V
Test 13 “Cumulative sum” test
1 | def cumulative_sums(self, bin_data: str, method="forward"): |
The next three tests (the “cumulative sum” test, the random offset test, and the variant random offset test) are the author’s favorite NIST statistical functions because they deal directly with the concept of random walks.
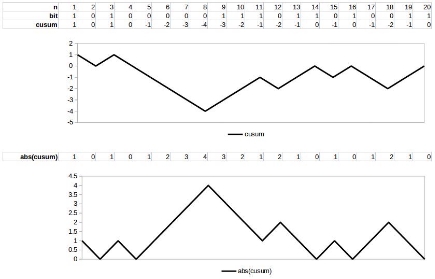
The “cumulative sum” test converts a random binary sequence into a random walk by replacing each 0-bit with (-1) and each 1-bit with (+1) and calculating the cumulative sum at each point along the sequence. Next, the test checks to see if the absolute maximum cumulative sum at any point along the sequence is within the range expected for a truly uniform random sequence. This process is shown in Figure 2-9.
Relating this test to the market, if the absolute peak (which may represent the bottom of a bull or bear market) is significantly higher or lower than expected, then this may indicate the presence of a variety of market phenomena, including bull/bear markets, cyclicality, regression to the mean, or momentum effects.
Test 14 Stochastic bias test
1 | def random_excursions(self, bin_data): |
Like the cumulative sum test, the random offset test deals with the concept of random walks, with the difference that the random offset test introduces the concepts of period and state. The difference is that the random shift test introduces the concepts of period and state. Period is any subsequence that starts and ends at 0, and state is the level of random walk at each moment. The states considered in this test are -4, -3, “, +3, +4. The test determines whether the number of visits to each state in each cycle is the same as would be expected from a uniform binary sequence.
test 15 Variant Random Offset Tests
1 | def random_excursions_variant(self, bin_data): |
The Variant Random Shift Test differs from the original in that it does not partition random walks and it counts the total number of times a random walk visited a wider range of random states, -9, -8,”, +8, +9, and the Random Shift Variant Test returns 18 p-values.
Test Procedure
After introducing the above stochasticity test function, we use actual financial market data for testing. First of all, we use the S&P 500 index for statistical testing due to the amount of data:
First, the closing price day data of S&P 500 index from 1928 to 2018 is collected, and the data volume is about 90 years.
Second, NIST tests are applied to a windowed sample of the original data. Therefore, these data are discretized and then split into windows. We chose a window period of 5 years.
Quantitative Trading Core Strategy Development: From Modeling to Practice! [ref3]
Third, the process used to generate the window is shown below and can also be found in the corresponding Python code:
(1) Read the data;
(2) Convert the sequence of exponential returns to a binary sequence using the discretization operation; (3) Calculate the number of binary bits in the sequence;
(4) Determine the number of years in the sequence;
(5) Specify the length of each window, w = 5;
(6) Determine how many binary numbers are in each window;
(7) Calculate the number of samples x;
(8) Divide the binary sequence into x samples;
(9) Apply each test to each sample and calculate the P value; (10) Determine the number of samples that pass. If the P value is less than 0.005 (99.5% confidence level), the sequence is
non-random;
(11) If the number of samples passing is greater than or equal to 90%, the randomness test is passed. Test code :
1 | import numpy |
2.3.4 Analysis of Results
Note that the NIST document suggests a standard of 96% of samples passing the test, rather than 90%. We have lowered this requirement (meaning that the market appears to be more likely to be verified as random) because of the relatively small number of samples that can be generated when using a non-overlapping sampling method on a shorter dataset.
Finally, the test results contain two additional simulated datasets for comparison. The first dataset is a binary sequence generated using the same discretization strategy on the output of the NumPy Mersenne Twister' algorithm. Mersenne Twister` is one of the best pseudo-random number generators, but it still does not achieve true randomness. The second dataset is a binary sequence generated from a deterministic function. These two datasets serve as a benchmark for comparison between completely random and completely deterministic sequences.
Showing results
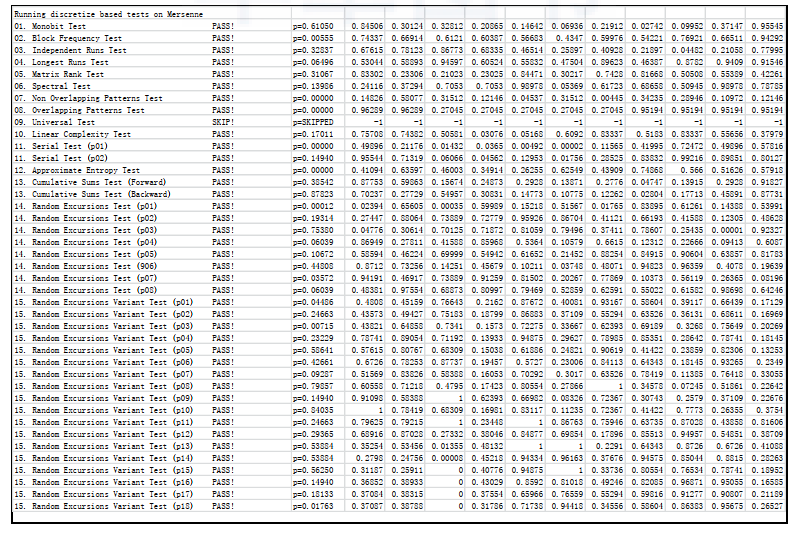
The results of the Mersenne Twister algorithm test are shown in Figure 2-10.
The results of the tests are shown in Figure 2-10, where almost all the samples pass all the tests, and each test concludes that the sequence is random because more than 90% of the samples pass each test.
Each number in the figure represents a P value. The test passes or fails depending on whether the P value is below a threshold of 0.005. Each column represents the results of the test for a window period (5 years). The first column after the test name indicates whether the test has passed (PASS!) or failed (FAIL!). A passed test tells us that the sequences are random, while a failed test tells us that there is a specific pattern in these sequences.
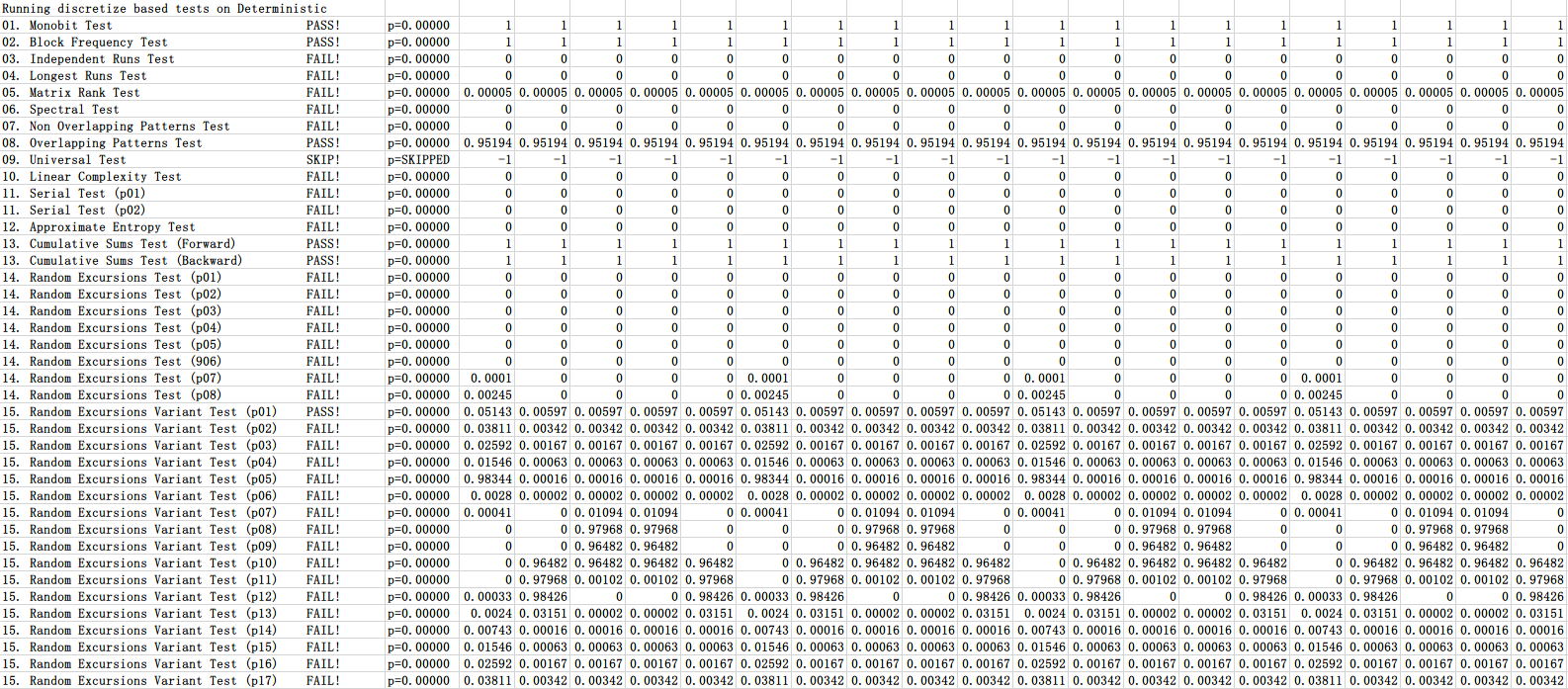
The results of the deterministic function are shown in Figure 2-11.
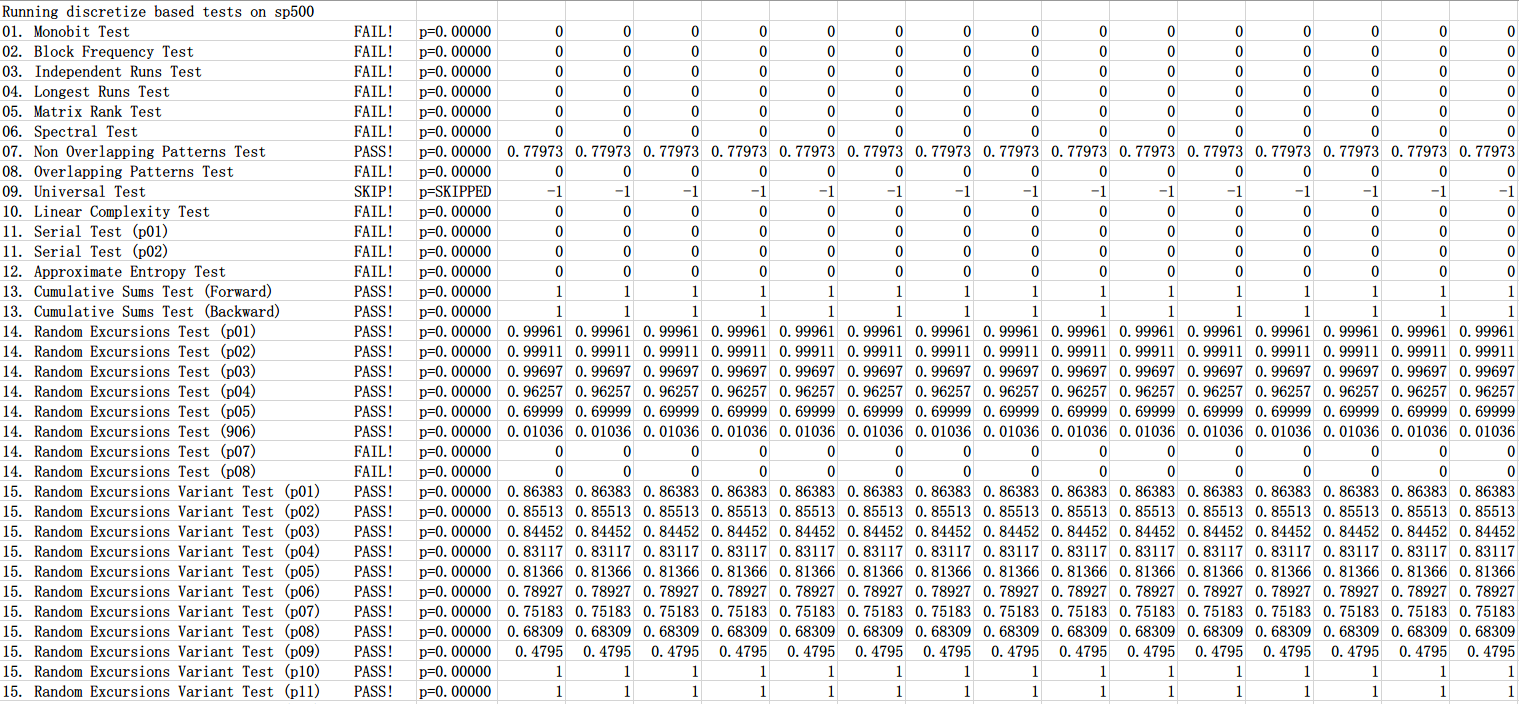
As can be seen in Figure 2-11, almost all of the sample fails the test. The results of the S&P 500 test are shown in Figure 2-12.
As can be seen in Figure 2-12, a significant portion of the sample failed the randomness test.
test results
The score for the S&P 500 dataset lies between the scores of the two benchmarks, meaning that the market is less random than the Mersenne Twister algorithm and more random than the deterministic function - but still not random.
Conclusion
At the beginning of this section, we told the story of how Prof. Burton Malkiel made it difficult for an unfortunate technical analysis expert to flip a coin. Prof. Malkiel compared the stock market to a game of coin flips and advocated a passive style of investing. While I have great respect for this professor, I believe this conclusion is wrong. What this story tells us is that in the eyes of a technical analyst, there is no difference between a coin flip and market price action. However, this does not mean that there is no difference between a coin flip and market price action in the eyes of a quantitative trader, or more specifically, a statistical test. In this subsection, I have shown that while it may not be possible to tell the difference personally (with my own two eyes), NIST’s randomness testing system certainly can. Because markets are not random.