Quantitative Trading Core Strategy Development Chapter 2_01

Chapter 2: Basic Perceptions of the Market

Most people don’t really understand the marvelous markets we are in. Starting with the efficient market hypothesis, this chapter explains the fundamental characteristics of the markets we live in: randomness, chaos, and time-varying nature, through the construction of stochastic portfolios, statistical tests of randomness, and the successes and failures of machine learning in the markets.

2.1 From EMH to AMH

What is the Efficient Market Hypothesis (EMH)? The essence of the theory can be gleaned from the following old joke.

`A 100 dollar bill is lying on the ground and an economist walks by it. A friend asks, “Did you see any money there?” The economist replied, “I thought I did, but I must be mistaken. If there had been $100 on the ground, then someone would have picked it up long ago.” ‘

As the joke implies, the efficient market hypothesis states that all information about a particular company has long been incorporated and reflected in its stock price. If stocks always traded at their fair value, investors would not be able to earn excess returns.

On a philosophical level, I do not fully agree with the efficient market hypothesis. Instead, I prefer the Adaptive Market Hypothesis (AMH) proposed by MIT professor Andrew Lo.

The EMH (Efficient Market Hypothesis) essentially assumes that market prices have reflected all available information. On the whole, investors are rational and any new information is quickly absorbed by the market, with the result that investors are usually unable to beat the market after accounting for taxes and transaction costs. Strict EMH believers believe that traditional active management is largely folly.EMH believers will only use low-cost index funds and strongly advocate the use of passive investing.

In contrast, AMH (Adaptive Market Hypothesis) takes the theory of EMH (Efficient Market Hypothesis) and adds a behavioral finance perspective.AMH theory assumes that successful investors will continue to apply their rules of thumb until they are eliminated by the market. Investors are neither rational nor irrational. Instead, investors are living creatures whose behavior is also influenced by evolution.

AMH has the following 5 corollaries.

• The relationship between risk and reward is not completely stable. It changes over time as the competitive environment changes.
• Active investment management can identify and capitalize on market inefficiencies from time to time.
• Adaptation and innovation are the keys to survival.
• Survival is the only goal that matters.
• No strategy will work all the time

2.2 We can’t beat all the monkeys

There is a seemingly absurd but true fact in the financial industry (see Figure 2-1):** In the financial markets, monkeys can outperform most fund managers** by tossing loose balls to pick stocks. While there are obvious advantages to hiring monkeys over fund managers, such as lower salaries and a higher work ethic, a random number generator is like a monkey rolling dice for asset management firms that can’t afford to work with primates over the long term.

In fact, even random number generators can and will outperform almost any fund. Such a randomized strategy may seem like a joke, but if a joke can outperform industry professionals, we must stop and think about what went wrong. When designing an investment strategy, it is useful to understand how stochastic strategies work and what kind of results they are likely to produce. Given that stochastic strategies typically perform well, they can serve as a valid performance benchmark….

2.2.1 Let’s start with a benchmark index

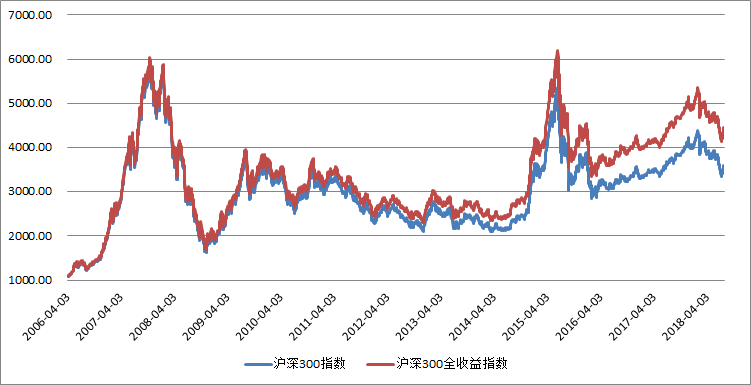
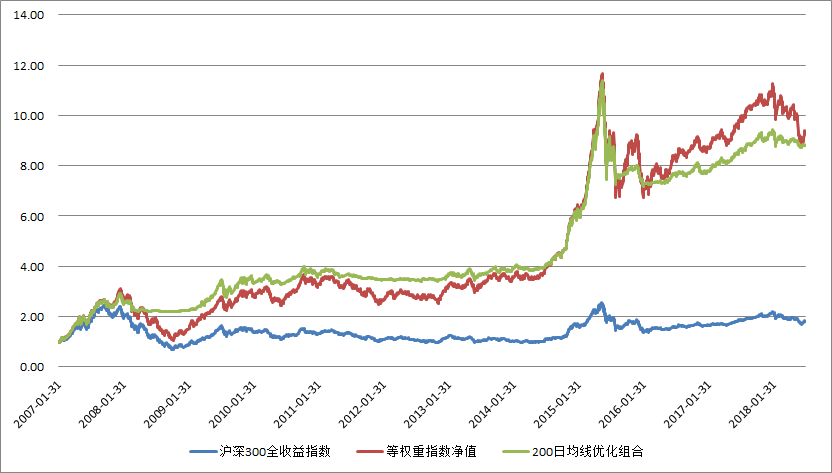
Every portfolio must have a benchmark index. Here we use the CSI 300, a common domestic benchmark. When we have a benchmark index, it is used to measure performance. For a (public) fund manager, it does not matter if the absolute return is +10% or -10% at the end of a year, rather, the performance relative to the benchmark index is important. The index we use in this article, the CSI 300 Total Return Index, is different from the normal CSI 300 index we often see. It is a total return index, meaning that all dividends are reinvested. So keep in mind that the CSI 300 Total Return Index will always perform better than a regular index (refer to Figure 2-2).

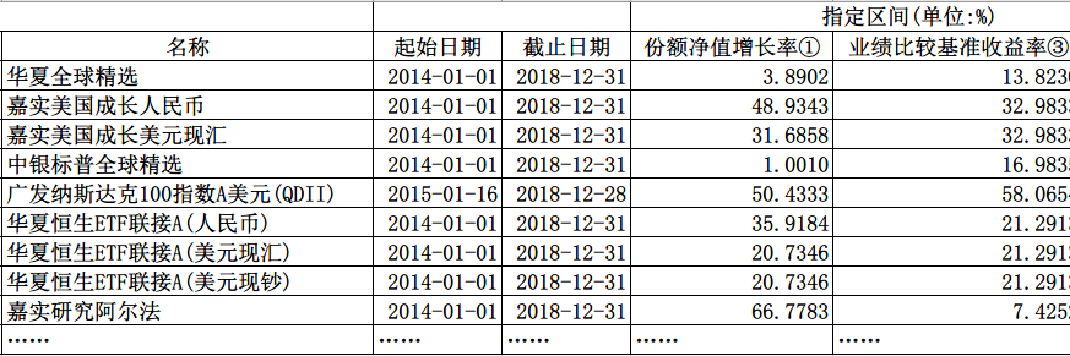
Table 2-1 shows the performance of domestic surviving funds for the last 5 years as of December 31, 2018 (only some are listed). Statistically, within the 460 equity funds in existence, only 54.35% beat the benchmark index over the last 5 years. Looks bad, right? But it’s far better than its counterparts across the pond. Only about 15% of fund managers in the U.S. manage to beat their benchmarks over a 5-year time horizon.

2.2.2 Constructing a Stochastic Portfolio

With the benchmark indexes taken care of, let’s get started. Here is how to construct the stochastic portfolio.

• Select stocks only from the constituents of the CSI 300 index.
• At the end of each month, the positions are balanced again.
• The position of each stock is randomized.

The code is as follows:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

%测试1 按月调仓，随机仓位
 weight=[];
jinzhi=ones(n,1);
for i=start:n
    %计算今日股票收益
    ret=data(i,:)./data(i-1,:);
    if isempty(weight)
        jinzhi(i)=jinzhi(i-1);
    else
       %计算今日基金净值
        weight=weight.*ret(today>0)';
       jinzhi(i)=sum(weight); 
    end
    if ismember(i,posx)%判断当天是否月末
       %遍历所有股票,选出200个交易日前已经上市的股票
       today=data(i-200,:);
       temp=today(today>0);
       price=data(i,today>0);
       num=length(temp);
       aa=rand(num,1);
       %随机分配仓位
       weight=aa./sum(aa)*jinzhi(i);

    end
    
end

The results are shown in Figure 2-3:

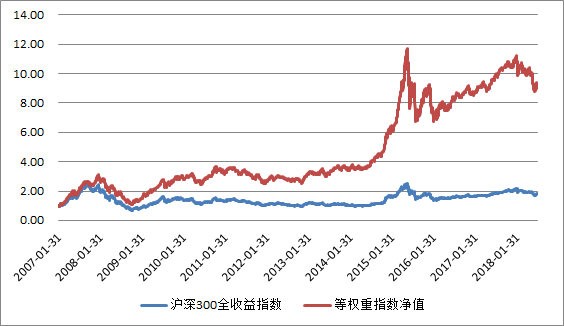
Surprisingly, the stochastic strategy has achieved much higher returns than the index. It has gained more than 100% over the last 5 years, beating a host of fund managers. Of the 460 stock funds in existence, only 4 have gained more than 100% over the last 5 years, meaning that the stochastic strategy beats more than 99% of fund managers.

Of course, there are some flaws in this test, such as survivor bias, which we’ll talk about later in the book. However, this does not affect our conclusions because the backtest results are so significant.

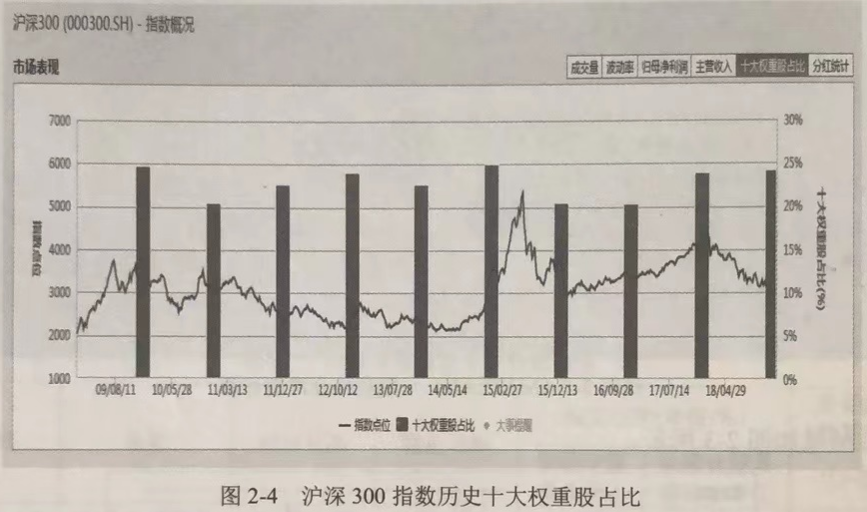
So, why are the backtest results so good? The key reason is that our portfolio positions are randomized and do not follow the market cap weighting rules of the CSI 300. By simply avoiding market capitalization weighting, we would have outperformed the broader market. We all know that there are 300 stocks in the CSI 300, but do we know that the top 10 stocks in the index have a weighting of about 25%? We all assume that the CSI 300 is a diversified index, which it is not. It primarily tracks a few of the largest companies in the market, and the rest are unimportant (see Figure 2-4).

To be fair to indices, I must point out that indices are not initially investment targets. They are meant to measure the health of the market, but that doesn’t mean we should invest like an index. It is easy to compare the investment results of an equal-weighted index to a market-capitalization-weighted index with the following code.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

jinzhi1=ones(n,1);
%测试2 按月调仓，平均仓位
weight=[];
for i=start:n
    %计算今日股票收益
    ret=data(i,:)./data(i-1,:);
    if isempty(weight)
        jinzhi1(i)=jinzhi1(i-1);
    else
        weight=weight.*ret(today>0)';
       jinzhi1(i)=sum(weight); 
    end
    if ismember(i,posx)%判断当天是否月末
       %遍历所有股票,选出200个交易日前已经上市的股票
       today=data(i-200,:);
       temp=today(today>0);
       num=length(temp);
       %平均分配持仓
       weight=ones(num,1)/num*jinzhi1(i);
    end
    
end
figure(2)
plot(benchmark./benchmark(503),'blue')
hold on
plot(jinzhi1,'red')

The results are shown in Figure 2-5.

In the stochastic simulation above, we have seen that both equal and random weights are superior to market value weights, and apparently only monkeys use random weights. Equal weights are common, but using some common tricks can obviously optimize the performance of the portfolio. Next, we move the portfolio using the methodology from Mebane TFaber’s SSRN #1 downloaded paper “A Quantitative Approach to Tactical Asset Allocation”.

• Selecting stocks only from the constituents of the CSI 300 Index.
• At the end of each month, the positions are rebalanced.
• Equal positions in each stock.
• The closing price of the day is compared to the 200-day SMA to determine whether to hold cash for the next month at a rate of 3% per annum.

The code is as follows.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

%测试3 按月调仓，平均仓位,按200日均线决定是否持有现金
jinzhi2=ones(n,1);
weight=[];
for i=start:n
    %计算今日股票收益
    ret=data(i,:)./data(i-1,:);
    if isempty(weight)
        jinzhi2(i)=jinzhi2(i-1);
    else
       ret2= ret(today>0);
       %将无风险收益赋值给相应资产
       ret2(compare)=risklessrate+1;
       weight=weight.*ret2';
       jinzhi2(i)=sum(weight); 
    end
    if ismember(i,posx)%判断当天是否月末
       %遍历所有股票,选出200个交易日前已经上市的股票
       today=data(i-200,:);
       ma200=sum(data(i-199:i,:))/200;
       temp=today(today>0);
       temp2=ma200(today>0);
       price=data(i,today>0);
       %找到今日收盘价小于200日均线的资产的index
       compare=find(price<temp2);
       num=length(temp);
       weight=ones(num,1)/num*jinzhi2(i);
    end
    
end
figure(3)
plot(benchmark./benchmark(503),'blue')
hold on
plot(jinzhi1,'red')
hold on
plot(jinzhi2,'green')

The results are shown in Figures 2-6.

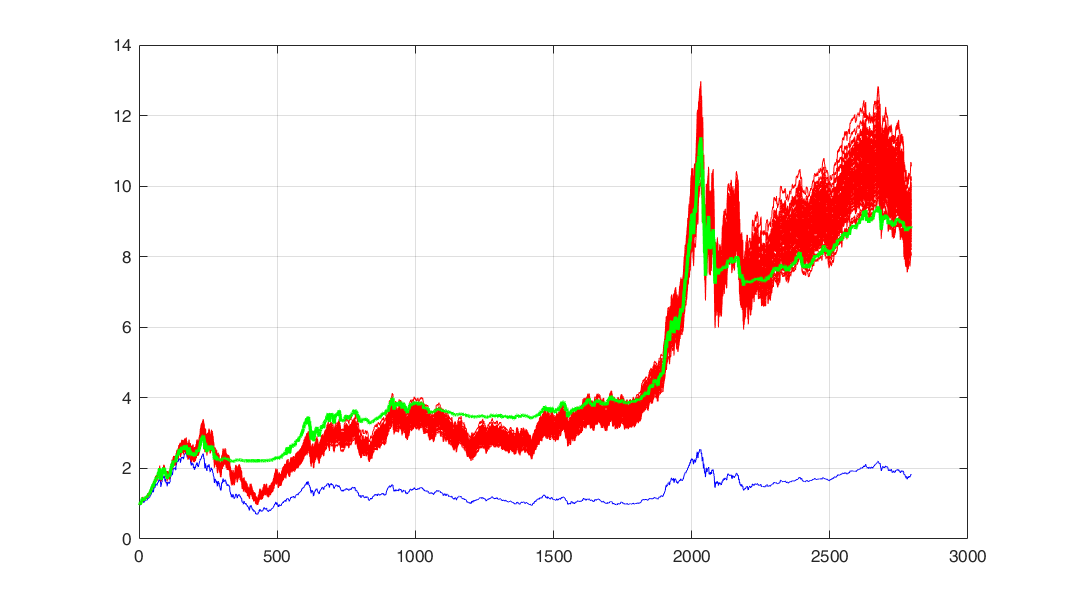
As you can see, after screening for the 200-day SMA, the portfolio’s return-to-risk ratio has improved dramatically. This looks good, so the key question is, how does this method compare to the monkey? We repeated Test 1 100 times and got the results shown in Figure 2-7.

As can be seen in Figure 2-7, although our optimized portfolio led all portfolios for a long historical period, in the end it was the random portfolio that prevailed.

2.2.3 Conclusion

Based on the above simulation test, we can get the following conclusion.

• It is very easy to simulate a net worth curve that outperforms the index.
• It makes more sense to use a stochastic model as a benchmark than an index.
• Trading systems do not improve returns, but they do improve the risk-return ratio.
• We will never beat all the monkeys.